Scientific notation

Scientific notation is a way to represent large and small numbers that is both easy to comprehend and also easy to do many math operations on them at the expense of limited precision.

Example

The world population is around 7.9 billion people. This number can be represented in standard form: 7, 900, 000, 000

Or using scientific notation: 7.9 ⋅ 10⁹

Another common example is a mass of an electron, which can be writen in standar form as: 0.00000000000000000000000000091g

Alternatively, we could use scientific notation and simply write: 9.1 ⋅ 10⁻²⁸g

I am sure you have seen it before. It is also pretty obvious why one would use such notation for writing. How about we also take a look at how this form could be useful for calculations.

Simplifying calculations

Let’s calculate the following: 14000000/0.000000007

We could try and solve it like we learnt in school:

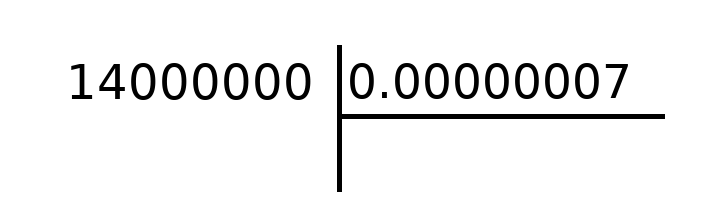
Honestly, I need a minute to count the amount of zeros here before even starting to comprehend the result.

Let’s write it in scientific notation instead. To do that, we are going to squish a number into two parts: significant numbers and it’s exponent:

14000000 → 14 * 10⁶

0.000000007 → 7 * 10⁻⁹

Now dividing these two numbers is way simpler, since we can use basic algebra to simplify exponents:

$$ \frac{14 \cdot 10^6}{7 \cdot 10^{-9}} = \frac{14}{7} \cdot 10^{6} \cdot 10^{9} = \frac{14}{7}\cdot10^{6+9} = 2 * 10^{15} $$

See, way easier!

Practical example

You may say: “How often do you need such calculations? For most cases standard notation is just fine”

Well, scientists most of the time deal with things that are either very small, like atoms, or very large, like stars and planets. How about we calculate gravitational force between Earth and Moon? Let’s write it down using conventional form first:

Let me remind you the formula: $$F = \frac{G \cdot m_1 \cdot m_2}{r^2}$$ Where:
F - gravitational force

G - universal gravitational constant = $$ 6.673 * 10^{-11} [\frac{Nm^2}{Kg^2}] $$

m - mass of an object
r - distance between objects

Moon mass is: 73420000000000000000000 (Kg)
Earth mass is: 5972000000000000000000000000 (Kg)
Distance: 360000000 (m)
Distance to the moon varies through year, but let’s calculate the maximum gravitational force, meaning, let’s take the smallest distance.

Let’s calculate write it down using standard notation: $$F=\frac{0.000000000006673*73420000000000000000000*5972000000000000000000000000}{360000000^2}$$

Good luck calculating that!

Now, let’s do the same but in scientific notation

$$F=\frac{6.673 \cdot 10^{-11} \cdot 7.342 \cdot 10^{22} \cdot 5.972 \cdot 10^{24}}{(3.6\cdot10^8)^2}$$

Here we can simplify the calculation by multiplying significand digits and exponent separately:

$$F=\frac{6.673 \cdot 7.342 \cdot 5.972 \cdot 10^{24+22-11}}{3.6^2\cdot10^{2\cdot8}}$$

$$F=\frac{292.59 \cdot 10^{35}}{3.6^2\cdot10^{16}}$$

$$F=\frac{292.59 \cdot 10^{35}}{12.96\cdot10^{16}}$$

$$F=\frac{292.59}{12.96} \cdot 10^{35-16}$$

$$ \begin{align} F=22.58 \cdot 10^{19} [N] \end{align} $$

Scientific notation simplifies many calculations for us.

Standard Scientific Notation (Normalized Notation)

The final result could be represented in several different ways: 22.58 ⋅ 10¹⁹ = 2258 ⋅ 10¹⁷ = 0.2258 ⋅ 10²¹

All of these are valid scientific notations. To reduce confusion and provide an easy way to quickly compare numbers, scientists have agreed on a format of Standard Scientific Notation, where only one whole number is used and it has to be between 1 and 9. Meaning, the standard representation of our result is: 2.258 ⋅ 10²⁰

E-notation

If we were to solve our problem with calculator, it would probably output result in what is called E-notation: 2.258e20

Since many devices and editors do not support superscript, you have two options:

1. Use caret “^” (aka carat, circumflex) character to denote an exponent.
   Examaple: 2.258 * 10 ^ 20
   Downside: this character also denotes XOR operation.
2. Use e-notation: 2.258e20

Formal definition

Now would be a good time to learn a few smart words. As we can see a number in scientific notation can be denoted as: m ⋅ 10ⁿ

We call m - mantissa or significand
n - exponent

And that’s everything there is to know about scientific notation

16 Mar 2022 - Hasan Al-Ammori